1.     Modern Symbolic Logic

Since the later decades the 19^th century, and more and more so throughout the 20^th century, “modern symbolic logic” has gradually discarded and displaced “classical formal logic.” What is the essential difference between them? Classical formal logic, which was discovered or invented by Aristotle (4^th century BCE) and further developed and improved on over time by many successors, is based on the idea of studying the logical properties of propositions by replacing material propositions with formal ones. A categorical proposition is formal, if its terms are variables instead of constants – e.g. “All X are Y” is formal, because the symbols X, Y represent in theory any terms that might arise in practice. A hypothetical proposition is formal, if its theses are variables instead of constants – e.g. “If X, then Y” is formal, because the symbols X, Y represent in theory any theses that might arise in practice.

Now, whereas classical logic symbolized terms and propositions, it did not similarly symbolize the other components of propositions, such as their quantities, their modalities or their relational operators. In “All X are Y,” the words “all” and “are” remained in ordinary language (in our case, plain English). Similarly, in “If X, then Y” the words “if” and “then” were not symbolized. In modern symbolic logic, on the other hand, the trend developed to symbolize every aspect of every proposition[1]. This was, to be sure, a new school of logic, which considered that only in this way could utter precision of language be achieved, and all ambiguity or equivocation be removed from human discourse. Modern symbolic logic, then, advocated the adoption of an altogether artificial language comparable to the language of mathematics.

Some of the pros and cons of this approach are immediately obvious[2]. One advantage of symbolization, already mentioned, is the sense of precision sometimes lacking in natural languages. However, this impression is surely illusory – for if one’s understanding of the matter at hand is vague and uncertain to start with, how can symbols improve on it? A patent disadvantage of symbolization is the esoteric nature of artificial language. Logic was originally intended as a teaching for the masses, or at least the intellectuals, to improve their daily thinking. Nowadays, logic has become the exclusive domain of a few specialists, and has little to do with human cognitive practice. Moreover, communication is not always easy even among symbolic logicians, because each of them quite naturally prefers a different set of symbols, so that there is in fact not one artificial language, but many of them. Another disadvantage is the slow adaptability of any artificial language to forms of discourse newly discovered in everyday usage. An example of this is the a fortiori argument, which is still without convincing symbolic expression.

The main activity of ‘modern logicians’ nowadays seems to be to translate ordinary language into their favorite symbolic language. Most of the time, they seem content to rewrite a perfectly comprehensible plain English sentence into a purely symbolic one, as if this is some great achievement that will earn them their place in history, or at least in the profession. Just that act of translation or rewriting in symbolic terms seems to satisfy and thrill them tremendously, as if it confers scientific status onto the sentence. Additionally, they resort to pompous terminology for window-dressing and intimidation purposes. One gets the impression that symbols play for them the role of magic incantations in ancient times – ‘abracadabra!’ they would chant in pursuit of mystical insights and powers.

But, think about it a moment. In truth, when modern logicians rewrite a sentence in symbolic terms they have achieved exactly nothing other than to use shorter ‘words’ (i.e. the symbols they invent) in place of ordinary words, and (ideally) drawn up a table telling us what symbols correspond to what ordinary words. All they have done is abbreviate the given sentence. Apparently, they are too lazy to write long sentences and prefer concise ones. They have produced no new information or insight. They cannot credibly argue that the ordinary language statement was essentially deficient, since it must have been understandable enough for them to have translated it into symbols. If it was understandable enough for them, why not for everyone else? What absolute need have we of the artificial language(s) they so insistently try to sell us?[3]

Moreover, note this well, whenever we (and they) read the symbolic statement they have concocted, our minds have to translate it back into ordinary language in order to understand it. We have to mentally repeatedly refer back to the ordinary language definitions of the symbols. We have to remember: “Oh! This funny symbol means so and so, and that weird doodle means this, and the zigzag means that,” and so forth. This means that our mental process of understanding is made more difficult and slowed down considerably. We are further from the object of study than we were to start with – more removed from the reality we are trying to think about. This increased distance and waste of time is not accidental or incidental, however – it serves to cloud the issues and prevent critical judgment. Errors are hidden from sight, and if we spot them we hardly dare point to them for fear of admitting we may have missed something. In this way, foolishness is perpetuated and spreads on.

But all that is not the worst of it. The worst of it is twofold. First, modern logicians usually symbolize much too soon, when their level of insight and analysis is still in its early stages. They typically do not give the subject-matter studied time to develop and mature in their own minds, but impatiently rush into their more orderly looking and comfortable world of symbols. The result is that their symbols are usually representative of a very naïve, elementary, immature level of understanding of the object at hand. Secondly, once their symbolic representation is done, it freezes all subsequent work at that childish level. Since the symbolization is already settled, all they can do is play around with it in different ways. All they can do is manipulate and reorder and recombine their symbols this way and that way, and this is what they pass the rest of their time doing. They cannot feed on new experiences and insights from the world out there or actual human discourse, since they have already confidently and reassuringly separated themselves from all that. Their symbols thus blind them and paralyze them. The paucity of their results testifies to it.

Another aspect of modern symbolic logic important to note is its pretensions of ‘axiomatization’. In classical formal logic, the Laws of Thought (Identity, Non-contradiction and the Excluded Middle) were sovereign; these were axioms in the original sense of irreducible primaries of rational knowledge, together constituting the very essence of logic. In syllogistic validation by Aristotle, all syllogisms could be reduced directly or ad absurdum to a minimum number of primary moods – mainly the first figure positive singular syllogism: “This S is M, and all M are P, therefore, this S is P.” The latter argument was not perceived as an axiom in its own right or even as an arbitrary convention, but as a logical insight in accord with the laws of thought that what is claimed applicable to a concept must be acknowledged to apply to the things it subsumes. The relation of human reasoning, and more deeply of formal logic, to the laws of thought was progressively ‘systematized’, but it was allowed to remain essentially open and flexible. Though integrated, it was not rigidly fixed, so as to allow for its constant evolution and adaptation as knowledge developed.

Modern logicians, on the other hand, focusing on the more geometrico, the method of proof used in Euclidean geometry, sought a more predictable and definitive arrangement of knowledge. Their simplistic minds demanded rigid rules and perfect orderliness. A hierarchy was established between thoughts – with those at the top of the hierarchy (the laws of thought) being viewed as ‘axioms’ and those lower down (syllogisms, and eventually similarly other arguments) as ‘theorems’. This may work well for mathematics, which is a relatively special science, but it caused havoc in general conceptual logic, which is the science of science. The question naturally arose as to where those apparent axioms came from and whether they could be replaced by contrary ones as was done in non-Euclidean geometry. It did not take long for these simpleminded people to decide that logic was a conventional mental game, with no apparent connection to the empirical world. This philosophy (known as Logical Positivism) was largely justified by Immanuel Kant’s analytic-synthetic dichotomy[4], so it could hardly be doubted.

What is lacking in this model of knowledge is the understanding that formal logic is not deduced from the laws of thought. The laws of thought are not premises of formal logic; they are not contents from which other contents are deduced. The laws of thought refer us to the autonomous logical insights through which we naturally judge what constitutes appropriate inference. They are what justifies the processes of deduction (and more broadly, of induction) from premises to conclusions. The forms of syllogism and other arguments are not deduced from the laws of thought. The forms are induced from actual thought contents. The thought contents can be judged correct or not without reference to the forms, using ad hoc logical insights. What formal logic does is simply collect under a number of headings recurring types of thoughts, so that again using ad hoc logical insights we can once and for all predict for each type of thought (e.g. syllogism 1/AAA) whether it is correct or not. There is in fact no appeal to general ‘laws of thought’ in this validation (or invalidation) process; honest ad hoc logical insights are sufficient. The ‘laws of thought’ are merely ex post facto typologies of ad hoc particular acts of logical insight. For that reason, they are not top premises is a geometrical model of knowledge.

The question these modern pseudo-logicians did not ask themselves, of course, is why their allegedly logical insights in the course of ‘axiomatization’ (including their skepticism towards the objectivity of the laws of thought) should be preferred to the logical insights of the ‘non-axiomatization’ logicians. Is any discussion of logic possible without use of logic? Can logicians ever rightly claim to transcend logic? Can they logically deride and nullify logic? For instance, some have argued that appeal to the laws of thought is either circular argument or infinite regression. They stopped their reflection there, and never asked themselves why the rejection of circular argument or infinite regression should be considered primary logical acts not needing justification, while the laws of thought are to be rejected precisely on the ground that (according to them) there are no logical acts not needing justification. Is that not a double standard (another primary logical insight)?[5]

The radical blunder of the Kantian legacy is the belief that there is such a thing a ‘purely analytic’ or ‘a priori’ knowledge. Logicians influenced by this inane idea remain blind to the empirical aspects of all knowledge development. Even apparently purely symbolic systems of logic rely on perceptions. Some symbols refer to concrete objects (e.g. individuals a, b) and some to abstract ones (e.g. classes x, y); but every symbol is, as well as a sign for something else, in itself a concrete object (whether as a bit of ink on paper, or of light on a computer screen, or as a shape conjured in our mind’s eye). If follows that symbolic formulas, whether inductively or deductively developed, always depend on some empirical observation. The observation of symbols is not a transcending of experience; it is an empirical process just like the observation of cows; it requires physical or mental perception. Thus, if I count symbolic entities or I imagine them collected together, that is not purely analytic work – it is quite synthetic work. Moreover, such logicians tend to ignore the countless memories, imaginations and rational insights that form the wordless background of all discourse concerning logic.

Clearly, axiomatization was a con-game on a grand scale, through which shallow but cunning pseudo-logicians wanted to take power in the domain of logic. And they have indeed managed to do that almost completely. But the fact remains that primary logical insights like the laws of thought, or the rejection of circularity, infinite regression and double standards, or again the acceptance of subsumption (syllogistic reasoning) and the many, many other foundations of human thought, are not open to doubt. No amount of ‘axiomatization’ can either prove or disprove them, because all proof and disproof depends on such insights to at all convince us. The conclusion to draw from that is certainly not relativism or conventionalism, for that too would be a claim to the validity of some logical insight – i.e. the insight that all insights are arbitrary must itself be arbitrary. Logic cannot be refuted by logic. Logic can however be justified, by honest acknowledgment that some thoughts are primary logical insights. And these insights, which together constitute what we call ‘human reason’, cannot all be listed in advance, but emerge over time as knowledge develops.

Aristotle said all that long ago, but many have preferred to ignore him or misrepresent him because they dearly want to belittle him and supplant him, being envious of his achievements. Consider for instance the following statement about the law of non-contradiction drawn from his Metaphysics (Book 4, part 3. Translated by W. D. Ross.):

“For a principle which every one must have who understands anything that is, is not a hypothesis; and that which every one must know who knows anything, he must already have when he comes to a special study. Evidently then such a principle is the most certain of all; which principle this is, let us proceed to say. It is, that the same attribute cannot at the same time belong and not belong to the same subject and in the same respect.” (Italics mine.)

As a result of symbolization and axiomatization, modern logic is essentially a deductive logic enterprise. However complicated or complex it may look, it is inevitably superficial and simplistic. Even when modern logicians pretend to discuss induction, they are stuck in deductive activities. Their ‘logic’ is thus more and more divorced from reality. For this reason their thinking on issues of metalogic is thoroughly relativistic. Things have to be the way they think they are, since symbols are somehow omniscient and omnipotent. They see no idiocy or harm in ‘paraconsistent logic’ (i.e. in breach of one or more of the laws of thought), since to them it is all a game with conventional symbols with no connection to any reality. When things do not fit into their preconceived schemes, they blithely force them in and use florid terminology to keep critical judgment at bay. They do not look upon practical deviations from their arbitrary theoretical constructs as problems, as signals that they have made mistakes somewhere on their way; they just add more symbols and make their theories more abstruse. Please don’t think I am exaggerating – that’s the way it is.

Why are so many people drawn to and impressed by modern symbolic logic? Part of the problem is of course that this is what the universities demand from their teaching staff and teach their students; papers have to be written in symbolic terms to be even considered. But why this preference? Perhaps because pages filled with esoteric symbols seem more ‘scientific’, reminding readers of mathematical formulae in the physical sciences. It matters little that in logical science the subjacent subject-matter becomes less transparent and comprehensible when translated into symbols. Indeed, part of the aim is to befuddle and intimidate the reader, so as to conceal weaknesses and faults in the treatment. The grandiloquent language is similarly useful as eyewash. Modern symbolic logic boasts of superiority to classical formal logic, to give itself authority; but the truth is that most good ideas the former has it has stolen from the latter, reworking them a little and renaming them to seem original and independent. The whole enterprise is a massive ongoing fraud; or, alternatively, a collective delusion of epidemic proportions.

I am not, of course, saying (as, no doubt, some will rush to accuse me of saying) that everything modern symbolic logic tells us is false and irrelevant, or stolen. What I am saying is that whatever is true and significant in it is certainly not due to symbolization and axiomatization, and can equally well be (could be and probably was) developed by classical formal logic. Moreover, to repeat, excessive symbolism tends to simplistically lump things together and gloss over important nuances, and condemns its users to rigid and abstract thinking processes out of touch with the empirical domain.

We have seen, in the course of the present treatise on a fortiori logic, how some budding or experienced logicians strayed or failed due to their attempt to solve problems by means of modern symbolic logic. In the following pages, I present some more examples of the relative ineffectiveness of modern symbolic logic compared to classical formal logic. I show how the issue of ‘existential import’ is far less significant that it is touted to be; how attempts to bypass the laws of thought are futile; how the liar paradox is not only due to self-reference; and how the Russell paradox is due to the acceptance of self-membership.

2.     The Existential Import Doctrine

A term is, nowadays, said to have ‘existential import’ if it is considered to have existing referents; otherwise, it is said to be ‘empty’ or a ‘null class’. For examples, ‘men’ has existential import, whereas ‘dragons’ does not. This concept is considered original and important, if not revolutionary, in modern symbolic logic; and it is often touted as proof of the superiority of that school over that of classical formal logic. We shall here examine and assess this claim. As we shall see, although the concept has some formal basis, it is in the last analysis logically trivial and cognitively not innocuous.

The founder of formal logic, Aristotle, apparently did not reflect on the issue of existential import and therefore built a logical system which did not address it. The issue began to be raised in the middle ages, but it was not till the latter half of the nineteenth century that it acquired the importance attached to it today by modern logicians.

a.         Based on Aristotle’s teaching, classical formal logic recognizes six basic categorical forms of proposition: the general affirmative, “All S are P” (A), which means that each and every S is P; the general negative, “No S is P” (E), which means that each and every S is not-P; the particular affirmative, “Some S are P” (I), which means that each of an indefinite number (one or more) of S is P; the particular negative, “Some S are not P” (O), which means that each of an indefinite number (one or more) of S is not-P; and the singular affirmative, “This S is P” (R), and the singular negative, “This S is not P” (G), which refer to a specifically pointed-to or at least thought-of individual instance. Note that general (also called universal) propositions and particular propositions are called plural, in contradistinction to singular ones[6]. The labels A, E, I, O, R and G come from the Latin words AffIRmo and nEGO; the first four are traditional, the last two (R and G) were introduced by me years ago[7].

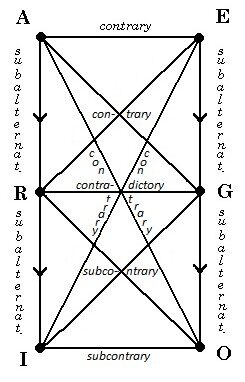
The symbols S and P stand for the subject and predicate. The verb relating them is called the copula, and may have positive (is or are) or negative (is not or are not) polarity[8]. In the present context, the copula should be understood very broadly, in a timeless sense[9]. When we say ‘is’ (or ‘is not’) we do not mean merely “is (or is not) now, at this precise time,” but more broadly “is (or is not) at some time, in the past and/or present and/or future.” The expressions ‘all’, ‘some’ and ‘this’ are called quantities. Obviously, the general ‘all’ covers every single instance, including necessarily ‘this’ specific instance; and ‘all’ and ‘this’ both imply the particular ‘some’, since it indefinitely includes ‘at least one’ instance. The ‘oppositions’ between the six forms, i.e. their logical interrelationships, are traditionally illustrated by means of the following ‘rectangle of oppositions’:

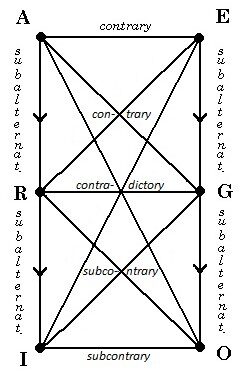
Diagram 29.1 – Aristotelian oppositions

Although Aristotle did not, to our knowledge, represent the oppositions by means of such a diagram, we can refer to it as a summary his views. It is taken for granted that, on the positive side A implies R and R implies I (so, A implies I), and on the negative side E implies G and G implies O (so, E implies O), although these implications cannot be reversed, i.e. I does not imply R or A, and R does not imply A, and so forth. This is called subalternation[10]. The core opposition in this diagram is the contradiction between R and G; from this assumption, and the said subalternations, all else logically follows[11]. A and O are contradictory, and so are E and I; A and E, A and G, E and R, are pairs of contraries; I and O, I and G, O and R, are pairs of subcontraries. Two propositions are contradictory if they cannot be both true and cannot be both false; they are contrary if they cannot be both true but may be both false; they are subcontrary if they may be both true but cannot be both false.

b.         Shockingly, the above traditional interpretation of the basic categorical forms (Diagram 29.1) has in modern times been found to be problematic. The above listed propositions are not as simple as they appear. The form “Some S are P” (I) means “Something is both S and P,” while the form “All S are P” (A) means “Something is both S and P, and nothing is both S and not-P;” similarly, the form “Some S are not P” (O) means “Something is both S and not-P,” while the form “No S is P” (E) means “Something is both S and not-P, and nothing is both S and P.” Seeing the forms I, A, O, E, in this more detailed manner, we can understand that A implies I since I is part of A (and likewise for E and O), but then we realize that A and O are not truly contradictories (and likewise for E and I).

The exact contradictory of “Something is both S and not-P” (O) is “Nothing is both S and not-P” (i.e. only part of A, with no mention of its I component) and the exact contradictory of “Something is both S and P, and nothing is both S and not-P” (A) is “Nothing is both S and P, and/or something is both S and not-P” (i.e. a disjunction including O, but also E). Note this well[12].

It should be pointed out that “All S are P” (A) can be defined more briefly as: “Something is S, and nothing is both S and not-P;” for given this information, it follows logically that the things that are S are P (for if this was denied, it would follow that some things are both S and not-P), Similarly, “No S is P” (E) can be defined more briefly as: “Something is S, and nothing is both S and P,” without need to specify explicitly that “Some things are both S and not-P.” Thus, all four forms A, E, I, O, imply, or presuppose (which is logically the same), that “some S exist(s).” Also, the positive forms, A and I, imply that “some P exist(s).” On the other hand, the negative forms, E and O, do not imply that “some P exist(s),” since the negation of a term is not informative regarding its affirmation[13].

Thus, in the above diagram, the diagonal links between the corners A and O, and between E and I, should not be contradiction but contrariety. For, while to affirm one proposition implies denial of its opposite, to deny one proposition does not imply affirmation of the other. To remedy this real problem of consistency, modern logicians have proposed to redefine the general propositions A and E as the exact contradictories of O and I, respectively. That is to say, the new meaning of A is only “Nothing is both S and not-P” and the new meaning of E is only “Nothing is both S and P.” It follows from this measure that A (in its new, slimmer sense) no longer implies I, and likewise E (in its new, slimmer sense) no longer implies O. This redefinition of symbols A and E can, to my mind, lead to much confusion. In my view, it would be better to re-label the forms involved as follows:

• Keep the traditional (old) labels A and E without change of meaning; i.e. old A = A, old E = E.
• Label the modern (new) senses of A and E as respectively not-O and not-I.
• That is, new ‘A’ = not-O ≠ old A. Whereas, old A = new ‘A’ plus I = I and not-O.
• Likewise, new ‘E’ = not-I ≠ old E. Whereas, old E = new ‘E’ plus I = O and not-I.

Thus, when we say A or E in the present paper, we mean exclusively the traditional A and E; and when we wish to speak of the modern ‘A’ and ‘E’ we simply say not-O and not-I, respectively. Note this convention well[14]. Actually, such propositional symbols are effectively abandoned in modern logic and the propositions are expressed by means of a symbolic notation, including the existential and universal quantifiers, ∃ (there exists) and ∀ (for all), respectively; but we do not need to get into the intricate details of that approach here, because we can readily discuss the issues of interest to us in plain English. Now, let us consider the formal consequences of the above findings in pictorial terms.

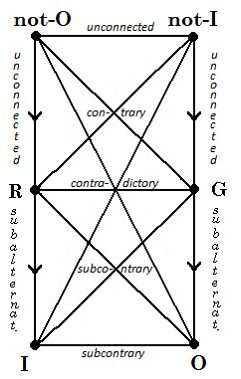
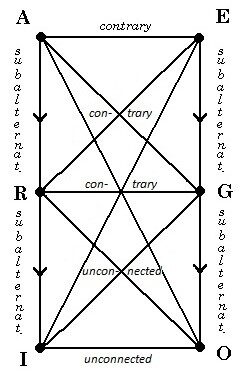
One way for us to solve the stated problem is to merely modify the traditional rectangle of oppositions, by showing the diagonal relationships between A and O and between E and I to be contrariety instead of contradiction; this restores the traditional diagram’s consistency, even if it somewhat dilutes its force (Diagram 29.2). Another possibility, which is the usual modern reaction, is to change the top two corners of the rectangle to not-O and not-I, instead of A and E respectively; this allows us to retain the contradiction between diagonally opposed corners, although now the lateral relation between the top corners is unconnectedness instead of contrariety, and the vertical relations in the upper square are unconnectedness instead of subalternation (Diagram 29.3).[15]

Notice that the lower square of the modern version is unchanged. This is due to the judgment that the forms I and O, i.e. “Something is both S and P” and “Something is both S and not-P,” both imply that “some S exist” (or “some things are S” or “there are things which are S”) meaning that if they are true, their subject ‘some S’ has existential import. Moreover, in the case of I, the predicate P is also implied to have existential import, since it is affirmed; but in the case of O, the predicate P is not implied to have existential import, since it is merely denied. Until now, note well, we have not mentioned the issue of existential import in our formal treatment. Now, it comes into play, with this interpretation of particular propositions.

The same applies to R and G – their subject ‘this S’ has existential import, whereas the predicate P has it if affirmed but lacks it if denied. On the other hand, since not-O (as distinct from A) is a negative statement, i.e. means “Nothing is both S and not-P,” it has no implication of existential import. Similarly, since not-I (as distinct from E) is a negative statement, i.e. means “Nothing is both S and P,” it has no implication of existential import. Clearly, if not-O was thought to be contrary to not-I, then if not-O were true, it would imply the negation of not-I, i.e. it would imply I; but this being erroneous, not-O and not-I cannot be contrary, i.e. they must be unconnected. Similarly, if not-O was assumed to imply R, it would then imply I, since R still implies I; therefore, not-O must also be unconnected to R; and similarly for not-I and G. On the other hand, not-O remains contrary to G, since if not-O is true, then O is false, in which case G must be false; similarly as regards not-I and R.

It is now easier to see why the traditional rectangle of oppositions (7.1) seemed right for centuries although it was strictly-speaking wrong. It was tacitly assumed when drawing it that the subjects of general propositions always have existential import, i.e. imply that “some S exist (s).” When this condition is granted, then in combination with it not-O becomes A and not-I becomes E, and A implies I and E implies O, and A exactly contradicts O and E exactly contradicts I – in other words we happily return to the original rectangle of oppositions (7.1). The problem is that this condition is not always satisfied in practice. That is, not-O or not-I can occur without their subject S having existential import.

Effectively, the forms “Nothing is both S and not-P” (not-O) and “nothing is both S and P” (not-I) signify conditional propositions (“Whatever is S, is P” and “Whatever is S, is not P”) which, without the minor premise “this is S,” cannot be made to conclude “this is P” or “this is not P” (respectively). In other words, they record a ‘connection’ between an antecedent and a consequent, but they have no ‘basis’, i.e. they contain no information affirming the antecedent, and thence the consequent. Obviously, if that information is provided, the condition is fulfilled and the result follows. Once we realize that the traditional rectangle remains true in the framework of a certain simple condition (viz. that some S exist), we see that its hidden ‘inconsistency’ is not such a big problem for formal logic.

It is interesting to also consider the significance of the above revisions in the field of eduction (i.e. immediate inference). Whereas A, which implies I (“Some S are P”), is convertible to “Some P are S” – not-O, which does not imply I, is not so convertible. Also, whereas not-I is convertible to “No P is S,” since “Nothing is S and P” and “Nothing is P and S” are equivalent and have no implication of existential import for S or P – E is not likewise unconditionally convertible, since in its case even if we are given that “some S exist” we cannot be sure that “some P exist” (but only that “some not-P exist”). Note well, just as O does not imply predicate P to have existential import, since it merely negates it, so is it true for E; therefore, the traditional conversion of E is really only valid conditionally. We can also look into the consequences of the above revisions in the field of syllogistic reasoning; the main ones are pointed out further on.

c.         Let us now go a step further in the possible critique of Aristotelian oppositions, and suggest that all terms may be denied to have existential import, whatever the forms they occur in, and whatever their positions therein. That is to say, not only the subjects of general propositions, but even the subjects of singular or particular propositions might conceivably lack existential import. Although R and G, and I and O, do formally imply that some S exist(s), it is still possible to deny them in pairs without self-contradiction. That is, R and G cannot be claimed strictly-speaking contradictory, because if “this S exists” is false then they are both false; this means that their traditional relation of contradiction is valid only conditionally (i.e. provided “this S exists” is true) and their absolute relation is in truth only contrariety. Similarly, I and O are only relatively subcontrary and their unconditional relation is really unconnectedness.

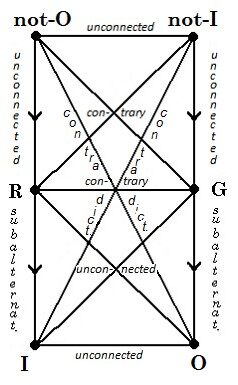
Indeed, it happens in practice that we reject a singular subject altogether, when we find that some predicate can be both affirmed and denied of it. This is dilemmatic argument: finding both that ‘this S’ is P and that it is not P, we must conclude that either one of these predications is wrong, or both are wrong because ‘this S’ does not exist. Particulars, of course, do not necessarily overlap; but if we can show by other means that “no S exists,” we can be sure that neither the set of S referred to by I nor that referred to by O exist, and thus deny both propositions at once. Granting all this, the above diagrams (7.2 and 7.3) can be further modified as follows:

In both these diagrams (7.4 and 7.5), all relations are the same as before, except the one between R and G (contrariety), and those between R and O, G and I, and I and O (which are now unconnected pairs). Notice that in the second diagram (7.5), although R and G are no longer contradictory, the pairs not-O and O, and not-I and I, remain contradictory, since if we deny that “Something is both S and P” (I) on the basis that “No S exists,” we can all the more be sure that “Nothing is both S and P” (not-I), and likewise regarding O and not-O.

d.         We have thus proposed two successive dilutions (weakening revisions) of the traditional rectangle of oppositions. In the first, we followed modern logic in no longer assuming with Aristotle that the subjects of universal propositions have existential import. In the second, we went further and additionally denied that singular and particular propositions may well lack existential import. Clearly, if our goal is to formulate an absolute logic, one applicable equally to propositions with existential import and those without, the successive dilutions of the Aristotelian diagram are justified and important. But are such logics of anything more than academic interest – are they of practical interest? The answer must clearly be no, as I will now explain.

A difficulty with the ideas of existential import and emptiness is immediately apparent: these are characterizations that may be true or false. Different people at the same time, or the same person at different times, may have different opinions as to the existential import or emptiness of a certain term. Some people used to think that dragons exist, and maybe some people still do, yet most people today think dragons never existed. So, these characterizations are not obvious or fixed. Yet modern logicians present the question of existence or non-existence as one which has a ready answer, which can be formally enshrined. They fail to see that the issue is not formal but contentual, and thus in every given material case subject to ordinary processes of testing and eventual confirmation or disconfirmation.

It follows that the issue of existential import is not as binary as it is made out to be. The issue is not simply existence or non-existence, as modern logicians present it. The issue is whether at a given time we know or not that existence or non-existence is applicable to the case at hand. A term with existential import may be said to be ‘realistic’, in that it refers (or is believed to refer) to some existing thing(s). An empty term, i.e. one without existential import, may be said to be ‘unrealistic’, in that it refers (or is believed to refer) to a non-existent thing. In between these two possibilities lies a third, namely that of ‘hypothetical’ terms, for which we have not yet settled the issue as to whether they are (in our opinion) realistic or unrealistic. Moreover, this third possibility is not monolithic like the other two, but comprises a host of different degrees.

Our knowledge is mostly based on experience of physical and mental phenomena, though also on logical insights relating to such experience. Roughly put, we would regard a term as realistic, if we have plentiful empirical evidence as to the existence of what it refers to, and little reason to doubt it. We would regard a term as unrealistic, if we have little empirical evidence as to the existence of what it refers to, and much reason to doubt it. And we would regard a term as hypothetical if we are thus far unable to decide whether it should be characterized this way or that. In any case, the decision is usually and mostly inductive rather than purely deductive as modern logicians effectively imagine it.

How are terms formed? Very often, a term is formed by giving a name to a circumscribed phenomenon or set of phenomena that we wish to think about. Here, the definition is fixed. More often, a term is applied tentatively to a phenomenon or set of phenomena, which we are not yet able to precisely and definitively circumscribe. In such case, we may tentatively define it and affirm it, but such a term is still vague as well as uncertain. Over time we may succeed in clarifying it and making it more credible. Here, the definition is variable. Thus, the formation of terms is usually not a simple matter, but an inductive process that takes time and whose success depends on the logical skills of the thinker(s) concerned.

Of course, as individuals we mostly, since our childhood, learn words from the people around us. This is effectively fixed-definition terminology for the individual, even if the term may have been developed originally as a variable-definition one. In this context, if we come across an obscure ready-made term, we cannot understand it till we find some dictionary definition of it or someone somehow points out for us the referent(s) intended by it. But even then, inductive acts are needed to understand the definition or the intent of the pointing. When you point at something, I cannot immediately be sure exactly what it is you are pointing at; I may have to ask you: ‘do you mean including this, excluding that?’ and thus gradually zero in on your true intent.

Each of us, at all times, retains the responsibility to judge the status of the terms he or she uses. The judgment as to whether a term is realistic, or unrealistic is not always easy. In practice, therefore, most terms are effectively hypothetical, whether classed as more probably realistic or more probably unrealistic. Even so, some terms are certainly realistic or unrealistic. All terms that are truly based exclusively on empirical evidence or whose denial is self-contradictory are certainly realistic, and all manifestly counterfactual or self-contradictory terms are certainly unrealistic. So, all three of these characterizations are needed and effective.

Let us suppose the formation of realistic terms is obvious enough, and ask how imaginary ones are formed. Imaginary terms are not formed ex nihilo; they are formed by combining old terms together in new ways. A new term T is imagined by means of two or more existing terms T1, T2…. We would call term T realistic, if all the terms (T1, T2…) constituting it are realistic and their combination is credible. But if all the terms on which T is based are realistic, but their combination is not credible (e.g. we know that no T1 is T2, so the conjunction T1 + T2 is contrary to fact), we would call T unrealistic; and of course, if one or more of the terms constituting T is/are unrealistic, we would call T unrealistic. If T is made up of hypothetical elements or if its elements are realistic but their combination is of uncertain status, we would call T hypothetical.

Now, our thinking in practice is aimed at knowledge of reality. That is to say, when we come across a term without existential import, i.e. when we decide that a term is unrealistic, whether because it goes against our empirical observations or because it is in some way illogical—we normally lose interest in it and drop it. We certainly do not waste our time wondering whether such a subject has or lacks some predicate, since obviously if the subject is non-existent it has no predicates anyway. If we regard a term as empty, the oppositions of its various quantities and polarities in relation to whatever predicate are henceforth totally irrelevant. An empty term, once established as such, or at least considered to be such, plays no further role in the pursuit of knowledge. This attitude is plain common sense, except perhaps for lunatics of various sorts. For this reason, the oppositions between propositions involving empty terms are trivial. That is, the above detailed non-Aristotelian models of opposition are insignificant.

The net effect of the successive ‘dilutions’ is to make the strong, Aristotelian rectangle of oppositions (concerning propositions with existential import) seem like a special case of little importance, and to give the weaker, non-Aristotelian rectangles (concerning variously empty propositions) a disproportional appearance of importance. The reason why this occurs is that the weaker oppositions represent the lowest common denominator between the Aristotelian and non-Aristotelian oppositions, which we need if we want to simultaneously discuss propositions with and without existential import. But the result is silly, for the Aristotelian diagram (7.1) is the important one, teaching us to think straight, whereas the non-Aristotelian ones are really of very minimal and tangential academic interest.

Practical logic is focused on terms that are believed to be realistic or at least hypothetical – it is not essentially concerned with empty terms. Contrary to the accusations made by modern logicians, Aristotelian logic is not only concerned with realistic terms. It is in fact mainly used with hypothetical terms, since (as already pointed out) most of the terms which furnish our thoughts are hypothetical – tentative constructs in an ongoing inductive enterprise. We do not think hypothetical thoughts by means of some special logic – we use the same old Aristotelian logic for them. That is to say, in accord with the principle of induction, we treat a hypothetical term as a realistic term until and unless we have reason to believe otherwise.

The reason we do so is that a hypothetical term, i.e. one not yet proved to be realistic or unrealistic, is a candidate for the status of realism. This being the case, we treat it as we would any realistic term, subjecting it to the strong, Aristotelian model of oppositions, rather than to any watered-down model with wider aspirations, in the way of an inductive test. If the hypothetical term is indeed deserving of realistic status, it will survive the trial; if, on the other hand, it does not deserve such status, it will hopefully eventually be found to lead to contradiction of some sort. In that event, we would decide that the hypothetical term should rather be classed as an unrealistic term, and we would naturally soon lose interest in it. Thus, there is only one significant and useful model for oppositions between propositions, namely the Aristotelian one.

Indeed, we sometimes use Aristotelian logic even for unrealistic terms. Very often, we remove the stigma of unrealism by rephrasing our statement more precisely[16]. Alternatively, we might just keep the imaginary intent in mind: say a novelist wishes to write about fictional people, or even science-fiction creatures, he would not logically treat his subjects as empty terms – but rather subject them to the logic applicable to realistic terms, so as to enhance the illusion of realism in his novel. Thus, the logic applicable to empty terms which we have above investigated is in practice never used.

Whatever the alleged existential import of the terms involved, our thoughts remain guided by the demanding model of Aristotelian oppositions. The rational pursuit of knowledge still indubitably requires the clear-cut logic of Aristotle enshrined in the traditional rectangle of oppositions (diagram 29.1). The reason why Aristotle took the existential import of the subjects of categorical propositions for granted is, I suggest, because naturally, if there is nothing (i.e. no subject) to talk about (i.e. to predicate something of) we will not talk about it; and if we are talking, then that presumably means we do have something to talk about, i.e. a subject as well as a (positive or negative) predicate. This is manifest common sense.

If Aristotle – as far as we know, or at least as far as readers of his extant works have so far managed to discern, or so we are told by historians of logic – did not ask the question regarding the existence of the subject, it is probably simply because he quite intelligently had no interest in empty subjects. He was rightly focused on the pursuit of knowledge of the world facing him, not some non-existent domain. Modern logicians are rather, I suggest, more intent on impressing the yokels with their intellectual brilliance. With that overriding purpose in mind, they fashion systems of no practical significance whatever. They make mountains out of molehills, presenting trivia as crucial discoveries, so as to draw attention to their own persons.

e.         Modern logic is a complex web of static relationships, most of them irrelevant. It ignores the dynamics of human thinking, the fact that our knowledge is constantly in flux. It is, we might say, a science of space irrespective of time. In an effort, on the surface praiseworthy, to formally acknowledge the issue of existential import, it gives undue attention to empty terms, elevating them from a very marginal problem to a central consideration. Instead of dealing with existential import parenthetically, as a side issue, it erects a logical system that effectively shunts aside some of the most important logical processes in the human cognitive arsenal.

The traditional universal propositions are cognitively of great importance. They cannot just be discarded, as modern logic has tried doing under the pretext that formal logic had to be expanded to include consideration of counterfactual terms. There are logical processes involving these propositional forms that are of great practical importance, and which logic must focus on and emphasize. It is absurd to henceforth effectively ignore these venerable and indispensable forms while making a big thing of a theoretical consideration of no practical significance whatever. The universals A and E cannot be retired under any pretext; they are not mere conventional conjunctions of more primitive forms.

For a start, universal propositions are essential to the crucial logical processes of subsumption and non-subsumption, which are enshrined in Aristotle’s syllogistic. First figure syllogisms serve to include an instance in a class or a subclass in a wider class; they teach us the notion that ‘all X’ includes every individual ‘this X’ and any possible set of ‘some X’. If, instead of an argument such as “All X are P and this S is X, therefore this S is P” (1/ARR) we propose the modern major premise “Nothing is X and not-P,” with the same minor premise, we obviously (even though the minor premise implies the existential import of an X) can no longer directly draw the desired conclusion! We are forced to stop and think about it, and infer that “this S is not not-P” before concluding that “this S is P.” Similarly, second figure syllogisms serve to exclude an instance from a class or a subclass from a wider class, and third figure syllogisms to identify overlaps between classes; and the moods of these figures become inhibited or greatly distorted if universal propositions are reinterpreted as modern logicians suggest.

Again, universal propositions are essential to the crucial logical processes of generalization and particularization. If ‘this X’ and ‘some X’ are not implied by ‘all X’, then we cannot generalize from the former to the latter. Of course, given ‘this X’ or ‘some X’, we do have existential import, and thus can anyway generalize to ‘all X’. But the fact remains that if, in accord with modern logic, we conceive our generalization as a movement of thought from “This/Some X is/are Y” to “Nothing is X and not-Y,” we miss the point entirely, even if admittedly the existential import of X is implied by the premise. For in such case, the formal continuity between premise and conclusion is lost, there being two inexplicable changes of polarity (from something to nothing and from Y to not-Y)! Similarly, particularization requires formal continuity. To move freely from I to A, and then possibly to IO, we need the traditional opposition (contradiction) between A and O.

Another issue that is ignored by modern logicians is modality. Although modern logic has developed modal logic to some extent, it has done so by means of symbolic notations based on very simplistic analyses of modality. Although it has conventionally identified the different categories of modality (necessity, impossibility, actuality, inactuality, possibility, unnecessity), it has not thoroughly understood them. It has not clearly identified and assimilated the different types of modality (the logical, extensional, natural, temporal, and spatial modes), even if human discourse has included them all since time immemorial. Notably lacking in its treatment is the awareness that modality is an expression of conditioning and that the different types of modality give rise to different types of conditioning.

Consideration of modality is manifestly absent in the doctrine of existential import. The latter (as we saw) is built around the timeless (or ‘omnitemporal’) forms of categorical proposition, which are non-modal. It does not apply to modal categorical propositions, for these do not formally imply (or presuppose) the actuality of their subject but only its possibility. Thus, a universal proposition with natural-modality, “All S can (or must) be P,” does not formally imply that “Some things are S” but only that “Some things can be S;” likewise, one with temporal modality, “All S are sometimes (or always) P” does not imply that “Some things are S” but only that “Some things are sometimes S;” and so forth.

This may be called ‘existential import’ in a broadened sense, acknowledging that being has degrees; but it is certainly not the actual sense intended by modern logicians: they apparently imagine that use of such modal propositions implies belief that “Some things are S.” And of course, the modality of subsumption, as I have called this phenomenon in my book Future Logic (chapter 41), is very relevant to the processes of opposition, eduction (immediate inferences), syllogistic deduction (mediate inference) and induction. Regarding the latter, see my detailed theory of factorial induction in the said work. Thus, we may well say that the proponents of the doctrine of existential import constructed an expanded system of logic based on a rather narrow vision of the scope of logic. Even if their expansion (for all it is worth—not much, I’d say) is applicable to non-modal propositions, it is not appropriate for modal ones.

f.          The critique of the Aristotelian rectangle of oppositions began apparently in the middle ages, with Peter Abelard (France, 1079-1142). According to the Kneales, further input on this issue was made over time by William of Shyreswood, by Peter of Spain and St. Vincent Ferrer, and by Leibniz. They also mention Boole’s interest in it, and many people attribute the modern view of the issue to this 19^th century logician. However, E. D. Buckner suggests that the modern idea stems rather from Franz Brentano (Austria, 1838-1917), in a paper published in 1874[17]. And of course, many big name logicians such as Frege and Russell have weighed in since then.

Even though the new logic that ensued, based on the concept of existential import, is today strongly entrenched in academia, the switchover to it was epistemologically clearly not only unnecessary but ill-advised. The doctrine of existential import has been woefully misnamed: it is in fact not about existential import, but rather about non-existential import. It gives to empty terms undue importance, and thus greatly diminishes the real importance of non-empty terms. To be sure, this innovation fitted the anti-rational ‘spirit of the times’, and it kept many people happily busy for over a century, and thus feeling they existed and were important – but it was in truth emptiness and vanity.

Apparently, none of these people reflected on the obvious fact that once a term is identified as empty, it is simply dumped – it does not continue affecting our reasoning in any significant manner. This being so, there is no need to abandon the universal forms A and E because they imply (presuppose) the existential import of their subject. Even if the Aristotelian framework, which is built around non-empty terms, occasionally ‘fails’ due to the appearance of an empty term in discourse, such event is taken in stride and dealt with by summarily eliminating the discredited term thenceforth, and certainly not by switching to a non-Aristotelian framework as modern logicians recommend to do. In any case, the issue of existential import does not apply to modal logic, and so lacks generality.

Moreover, these people failed to realize that Aristotelian logical processing relates not only to realistic terms, but more significantly to hypothetical terms, i.e. terms in process. They viewed logic as a deductive activity; they did not realize its essentially inductive character. If, due to an immoderate interest in empty terms, the science of logic abandons the universal forms A and E, it deprives people of a language with which to accurately express the movements of thought inherent in the processes of syllogistic inference and of generalization and particularization. The science of logic must acknowledge the forms of actual human thinking, and not seek to impose artificial contraptions of no practical value. Otherwise, natural processes essential to human cognition cannot be credibly expressed and logic will seem obscure and arbitrary.

Modern logic has sown confusion in many people’s minds, turning the West from a culture of confident reason to one of neurotic unreason. The purpose of logic studies ought to be to cognitively empower people, not incapacitate them. If logicians err in the forms of thought they describe and prescribe, they betray their mission, which is to intelligently and benevolently guide and improve human thinking. If they err, whether out of stupidity or malice, they turn logic from a responsible science and a fine art to a vain and dangerous game. They do not merely cease benefitting mankind; they positively harm people’s minds.